Exercice N°1

Soit la fonction définie sur $\mathbb{R}$ par : $$ \begin{cases} f(x)=\dfrac{1+\sqrt{x}\cos x}{x+2} & \text{si $x\geqslant 0$} \\ f(x)=\dfrac{x^{2}}{4\left( \sqrt{x^{2}+1}-1\right) } & \text{si $x < 0$} \end{cases} $$

• 1$°$)
  1. (a) Montrer que $f$ est continue en $0.$ Rappel

     Définition de continuité d'une fonction $f$ en un point $a$

     Correction

     On a $f$ définie continue sur $]-\infty ;0]$, alors $f$ continue à gauche
     en $0$ et $f(0)=\dfrac{1}{2}$.
     $\begin{eqnarray} \displaystyle\lim_{x\to 0^{+}}f(x)&=&\displaystyle\lim_{x\to 0^{+}}\dfrac{x^2}{4(\sqrt{x^2+1}-1)}\\ &=&\displaystyle\lim_{x\to 0^{+}}\dfrac{x^2(\sqrt{x^2+1}+1)}{4(\sqrt{x^2+1}-1)(\sqrt{x^2+1}+1)}\\ &=&\displaystyle\lim_{x\to 0^{+}}\dfrac{x^2(\sqrt{x^2+1}+1)}{4x^2}\\ &=&\displaystyle\lim_{x\to 0^{+}}\dfrac{\sqrt{x^2+1}+1}{4}\\ &=&\dfrac{1}{2} \end{eqnarray}$
     Puisque $\displaystyle\lim_{x\to 0^{+}}f(x)=f(0)$, alors $f$ est continue à droite en $0$.
     On a :$$\displaystyle\lim_{x\to 0^{-}}f(x)=\displaystyle\lim_{x\to 0^{+}}f(x)=f(0)$$ Donc f continue en $0$.

  2. (b) En déduire $\displaystyle\lim_{x\to \tfrac{\pi }{2}^{+}} \dfrac{\cos ^{2}x}{4\left( \sqrt{\cos ^{2}x+1}-1\right) }.$ Rappel

     Limite d'une fonction composée

     Théorème (admis)

     Soit $f$ et $g$ deux fonctions. Soit $a, b$ et $c$ finis ou infinis. Si $\displaystyle\lim_{x\to a}f(x)=b$ et $\displaystyle\lim_{x\to b}g(x)=c$ alors $\displaystyle\lim_{x\to a}g\circ f(x)=c$

     Correction

     La fonction $u : x\longmapsto \cos x$ est définie continue sur $\mathbb{R}$ et $\displaystyle\lim_{x\to \frac{\pi}{2}^+}\cos x=0^-$, car si $x\in ]\pi;\dfrac{\pi}{2}[$, $\cos x < 0$.
     De plus, $\displaystyle\lim_{x\to 0^-}f(x)=\dfrac{1}{2}$ alors $\displaystyle\lim_{x\to \frac{\pi}{2}^+}f\circ u(x)=\dfrac{1}{2}$.
     Pour tout $x < 0$, $f(x)=\dfrac{x^2}{4(\sqrt{x^2+1}-1)}$.
     D'où $f\circ u(x)=f(x)=\dfrac{\cos^2 x}{4(\sqrt{\cos^2 x+1}-1)}$
     Donc

     $\displaystyle\lim_{x\to \tfrac{\pi }{2}^{+}} \dfrac{\cos ^{2}x}{4\left( \sqrt{\cos ^{2}x+1}-1\right) }=\dfrac{1}{2}$.

• 2$°$)
  1. (a) Montrer que pour tout réel $x$ positif, on a : $\dfrac{1-\sqrt{x}}{x+2}\leqslant f(x)\leqslant \dfrac{1+\sqrt{x}}{x+2}.$ Rappel
     Pour tout $x\in \mathbb{R},\, \, -1\leqslant \cos x \leqslant 1$.
     Correction

     Pour tout $x\geqslant 0$, $\begin{eqnarray} -1\leqslant \cos x \leqslant 1 &\Longleftrightarrow& -\sqrt{x}\leqslant \sqrt{x}\cos x \leqslant \sqrt{x}\\ &\Longleftrightarrow&1-\sqrt{x}\leqslant 1+\sqrt{x}\cos x \leqslant 1+\sqrt{x}\\ &\Longleftrightarrow&\dfrac{1-\sqrt{x}}{x+2}\leqslant \dfrac{1+\sqrt{x}\cos x}{x+2}\leqslant \dfrac{1+\sqrt{x}}{x+2}\, \, (x\geqslant 0)\\ &\Longleftrightarrow&\dfrac{1-\sqrt{x}}{x+2}\leqslant f(x)\leqslant \dfrac{1+\sqrt{x}}{x+2} \end{eqnarray}$

     Donc pour tout réel $x$ positif, on a $\dfrac{1-\sqrt{x}}{x+2}\leqslant f(x)\leqslant \dfrac{1+\sqrt{x}}{x+2}$

  2. (b) En déduire que $\underset{x\rightarrow +\infty }{\lim }f(x)=0.$ Rappel

     Limite et ordre

     Théorème (admis)

     Soit $f, g$ et $h$ trois fonctions sur un intervalle I sauf peut-être en un réel $a$ de I.
     Soit $l$ un réel.
     Si $g(x)\leqslant f(x)\leqslant h(x)$ pour tout $x\neq a$ et si $\displaystyle\lim_{a}g(x)=\displaystyle\lim_{a}h(x)=l$, alors $\displaystyle\lim_{a}f(x)=l$

     Correction

     $\displaystyle\lim_{x\to +\infty}\dfrac{1-\sqrt{x}}{x+2}=\displaystyle\lim_{x\to +\infty}\dfrac{1+\sqrt{x}}{x+2}=\displaystyle\lim_{x\to +\infty}\dfrac{\pm 1}{\sqrt{x}}=0$.
     Puisque pour tout $x\geqslant 0$, $\dfrac{1-\sqrt{x}}{x+2}\leqslant f(x)\leqslant \dfrac{1+\sqrt{x}}{x+2}$.
     Alors :

     $\displaystyle\lim_{x\to +\infty}f(x)=0$

• 3$°$) Montrer que l'équation $f(x)=0$ admet au moins une solution $\alpha $ dans $\left] \dfrac{\pi }{2},\pi \right[ .$ Rappel

  Le théorème des valeurs intermédiaires

  Si la fonction $f$ est continue sur $[a ; b]$, alors $f$ prend au moins une fois toute valeur comprise entre $f(a)$ et $f(b)$.

  ce qui signifie que quel que soit le réel $k$ compris entre $f(a)$ et $f(b)$, l'équation $f(c) = k$ a au moins une solution dans l'intervalle $[a ; b]$.

  
  Correction

  $f$ est continue sur $\left] \dfrac{\pi}{2},\pi \right[$.
  Pour tout $x\in \left] \dfrac{\pi}{2},\pi \right[$, $x>0$ alors $f\left( \dfrac{\pi}{2} \right)=\dfrac{1+\sqrt{\frac{\pi}{2}}\cos \frac{\pi}{2}}{\frac{\pi}{2}+2}=0.28>0$ et $f(\pi)=\dfrac{1+\sqrt{\pi}\cos \pi}{\pi+2}=-0.15< 0$.
  D'après le théorème des valeures intermédiaires :
  

  On a $f$ est continue sur $\left] \dfrac{\pi}{2},\pi \right[$ de plus $f\left( \dfrac{\pi}{2} \right)f(\pi)< 0$ alors l'équation $f(x)=0$ admet au moins une solution $\alpha$ dans $\left] \dfrac{\pi}{2},\pi \right[$.

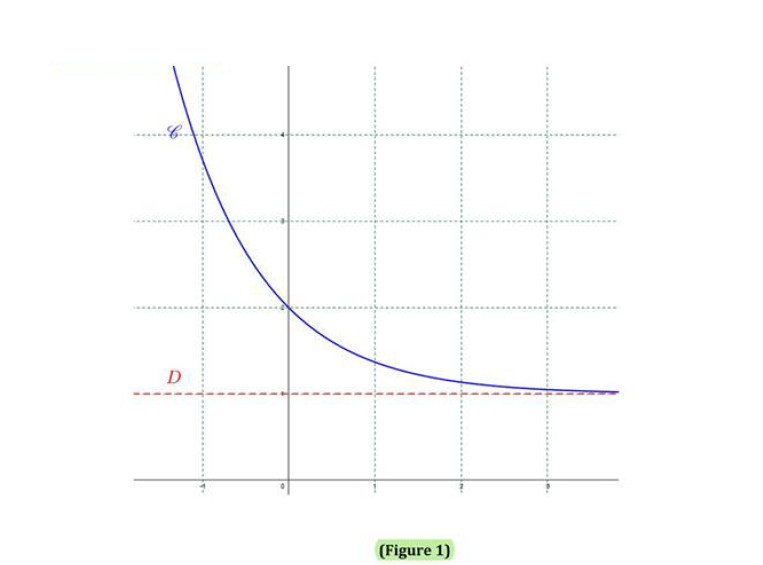
• 4$°$) La courbe ci-jointe $\textbf{(Figure 1 page 4)}$ représente une fonction $g$ dérivable sur $\mathbb{R}$ et qui admet la droite $D:$ $y=1$ comme asymptote horizontale au voisinage de $+\infty $ et une branche parabolique de direction $\left( Oy\right) $ au voisinage de $-\infty .$
  1. (a) A l'aide d'une lecture graphique :
     1. i/ Dresser le tableau de variation de la fonction $g$ et préciser $g\left( \mathbb{R} \right) .$ Rappel

        Image d'un intervalle par une fonction strictement monotone

        

        Correction

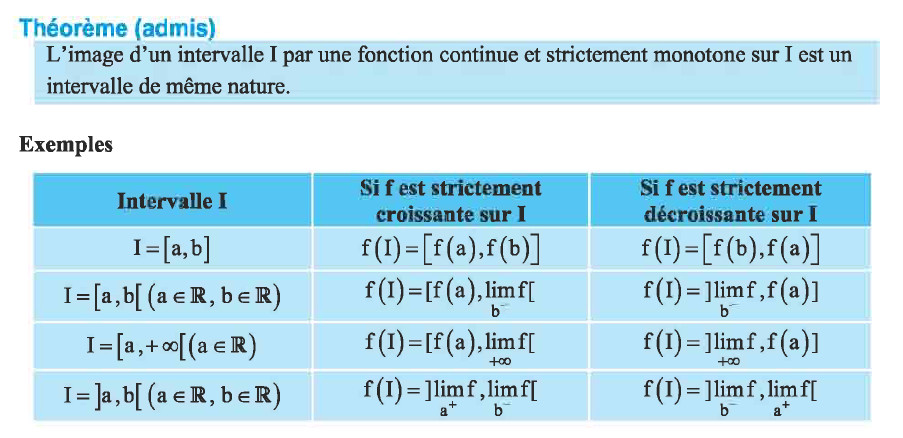
        Lecture graphique

     2. ii/ Prouver que l'équation $g(x)=\alpha $ admet une unique solution $\beta $ dans $\mathbb{R}.$ Rappel

        Théorème

        

        Correction

        $g$ est continue et strictement décroissante sur $\mathbb{R}$ et $g(\mathbb{R})=]1;+\infty[$. $\alpha \in \left] \dfrac{\pi}{2},\pi \right[$ alors $\alpha \in ]1;+\infty[$
        

        Donc l'équation $g(x)=\alpha$ admet une unique solution $\beta$ dans $\mathbb{R}$.

  2. (b)
     1. i/ Calculer $\displaystyle\lim_{x\to +\infty }g\circ f(x),$ $\displaystyle\lim_{x\to -\infty }f\circ g(x)$ et $\displaystyle\lim_{x\to 2020^{-}}g\left( \dfrac{2019x}{2020-x} \right) .$ Rappel

        Limite d'une fonction composée

        Théorème (admis)

        Soit $f$ et $g$ deux fonctions. Soit $a, b$ et $c$ finis ou infinis. Si $\displaystyle\lim_{x\to a}f(x)=b$ et $\displaystyle\lim_{x\to b}g(x)=c$ alors $\displaystyle\lim_{x\to a}g\circ f(x)=c$

        Correction

        1. On a $\displaystyle\lim_{x\to +\infty }f(x)=0$ et $\displaystyle\lim_{x\to 0 }g(x)=g(0)=2$ alors
           $\displaystyle\lim_{x\to +\infty }g\circ f(x)=2$.
        2. On a $\displaystyle\lim_{x\to -\infty }g(x)=+\infty$ et $\displaystyle\lim_{x\to +\infty }f(x)=0$ alors
           $\displaystyle\lim_{x\to -\infty }f\circ g(x)=0$.
        3. On a $\displaystyle\lim_{x\to 2020^- }\dfrac{2019x}{2020-x}=+\infty$ et $\displaystyle\lim_{x\to +\infty }g(x)=1$ alors
           $\displaystyle\lim_{x\to 2020^{-}}g\left( \dfrac{2019x}{2020-x} \right)=1$.

     2. ii/ Démontrer que $\tan \left( g\left( \beta \right) \right) =-\sqrt{\alpha -1}.$ Rappel

        Pour tout $x\neq \dfrac{\pi}{2}+2k\pi$, $\tan(x)=\dfrac{\sin x}{\cos x}$

        Pour tout $x\neq \dfrac{\pi}{2}+2k\pi$, $1+\tan^2(x)=\dfrac{1}{\cos^2 x}$

        1ère méthode

        1ère méthode

        On a $g(\beta)=\alpha \geqslant 0$ et $f(\alpha)=0$ alors $\dfrac{1+\sqrt{\alpha}\cos \alpha}{\alpha +2}=0$ d'où $\cos \alpha =-\dfrac{1}{\sqrt{\alpha}}$.
        Par suite $1-\cos^2 \alpha =1-\dfrac{1}{\alpha}=\dfrac{\alpha -1}{\alpha}$ alors $\sin \alpha =\dfrac{\sqrt{\alpha -1}}{\sqrt{\alpha}}$.
        Donc

        $\tan (g(\beta)) = \tan \alpha =\dfrac{\sin \alpha}{\cos \alpha}=\dfrac{\dfrac{\sqrt{\alpha -1}}{\sqrt{\alpha}}}{-\dfrac{1}{\sqrt{\alpha}}}$ alors $\tan (g(\beta))=-\sqrt{\alpha -1}$.

        2ème méthode

        2ème méthode

        On a $g(\beta)=\alpha \geqslant 0$ et $f(\alpha)=0$ alors $\dfrac{1+\sqrt{\alpha}\cos \alpha}{\alpha +2}=0$ d'où $\cos \alpha =-\dfrac{1}{\sqrt{\alpha}}$.
        Par suite $\dfrac{1}{\cos^2 \alpha} =\alpha$ alors $1+\tan^2 \alpha = \dfrac{1}{\cos^2 \alpha} =\alpha $.
        Alors $\tan (g(\beta)) = \tan \alpha =\sqrt{\alpha -1}$ ou $\tan (g(\beta)) = \tan \alpha =-\sqrt{\alpha -1}$.
        Puisque $\alpha \in \left] \dfrac{\pi}{2},\pi \right[$ alors $\tan \alpha \leqslant 0$.
        Donc

        $\tan \left( g\left( \beta \right) \right) =-\sqrt{\alpha -1}$.

Exercice N°2

• I-

  On considère, dans l'ensemble $\mathbb{C}$
  l'équation (E) : $\dfrac{1}{4}z^2-\sqrt{2}e^{i\frac{3\pi}{4}}z-i=0$.

  • 1°) Vérifier que : $z_1=\left( 2\sqrt{2}+2 \right)e^{i\frac{3\pi}{4}}$ est une solution de l'équation (E) Correction

    (E) : $\dfrac{1}{4}z^2-\sqrt{2}e^{i\frac{3\pi}{4}}z-i=0$.
    Pour $z=z_1=\left( 2\sqrt{2}+2 \right)e^{i\frac{3\pi}{4}}$ On a :
    $\dfrac{1}{4}\left( \left( 2\sqrt{2}+2 \right)e^{i\frac{3\pi}{4}} \right)^2-\sqrt{2}e^{i\frac{3\pi}{4}}\left( \left( 2\sqrt{2}+2 \right)e^{i\frac{3\pi}{4}} \right)-i=$
    $ \left( 3+2\sqrt{2} \right)e^{i\frac{3\pi}{2}}-\left( 4+2\sqrt{2} \right)e^{i\frac{3\pi}{2}}-i=$
    $-(e^{i\frac{3\pi}{2}})-i=-(-i)-i=i-i=0$ alors

    $z_1$ est une solution de l'équation (E) .

  • 2°) Déterminer alors l'autre solution $z_2$ de l'équation (E), puis vérifier que : $z_2=\left( 2\sqrt{2}-2 \right)e^{i\frac{3\pi}{4}}$. Rappel

    Somme et produit des racines d'un trinôme

    Soit $ax^2+bx+c$ un trinôme et $x_1, x_2$ ces deux racine alors :
    

    • $\colorbox{yellow}{$x_1.x_2=\dfrac{c}{a}$}$
    • $\colorbox{yellow}{$x_1+x_2=-\dfrac{b}{a}$}$
    Correction

    1ère méthode : (produit des racines)

    On a $z_1.z_2=\dfrac{c}{a}=\dfrac{-i}{\frac{1}{4}}=-4i$ alors $z_2=\dfrac{-4i}{z_1}=\dfrac{-4i}{\left( 2\sqrt{2}+2 \right)e^{i\frac{3\pi}{4}}}=\dfrac{4(2\sqrt{2}-2)}{4}e^{i\frac{3\pi}{4}}=\colorbox{yellow}{$\left( 2\sqrt{2}-2 \right)e^{i\frac{3\pi}{4}}$}$

    2ème méthode : (somme des racines)

    On a $z_1+z_2=-\dfrac{b}{a}=-\dfrac{-\sqrt{2}e^{i\frac{3\pi}{4}}}{\frac{1}{4}}=4\sqrt{2}e^{i\frac{3\pi}{4}}$ alors $z_2=4\sqrt{2}e^{i\frac{3\pi}{4}}-\left( 2\sqrt{2}+2 \right)e^{i\frac{3\pi}{4}}=\left( 4\sqrt{2}-2\sqrt{2}-2 \right)e^{i\frac{3\pi}{4}}=$ $\colorbox{yellow}{$\left( 2\sqrt{2}-2 \right)e^{i\frac{3\pi}{4}}$}$

• II-

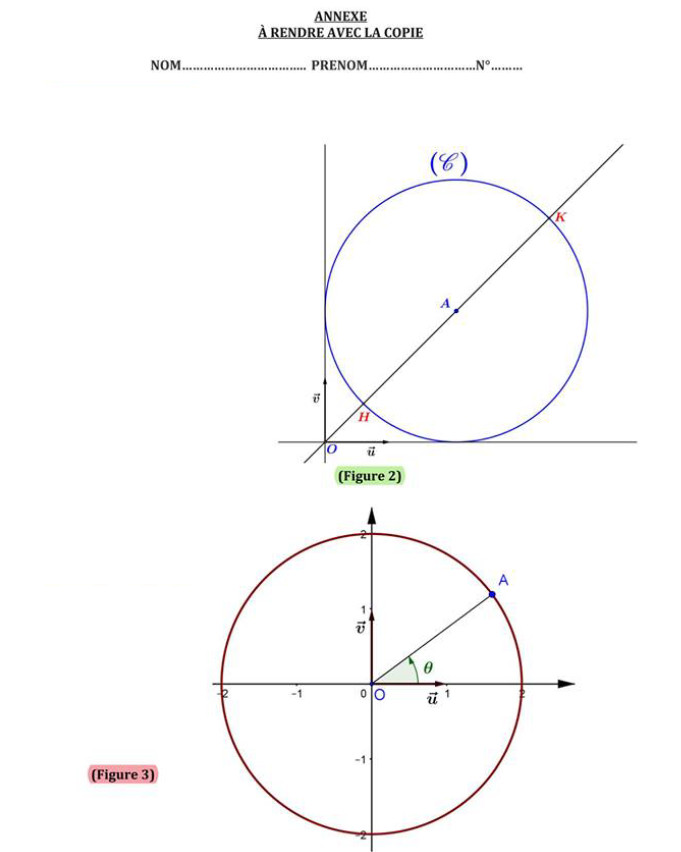
  Dant le plan complexe rapporté à un repère orthonormé $\left( O,\overrightarrow{u},\overrightarrow{v} \right)$. $\textbf{(Figure 2)}$
  Soit $A$ le point d'affixe $z_A=2+2i$ et $\Gamma$ le cercle de centre $A$ et de rayon $2$.
  La droite $(OA)$ coupe $\Gamma$ en deux point $H$ et $K$ tels que $OH< OK$. $\textbf{(Figure 2)}$

  • 1°) Montrer que : $z_H=\left( 2\sqrt{2}-2 \right)e^{i\frac{\pi}{4}}$ et $z_K=\left( 2\sqrt{2}+2 \right)e^{i\frac{\pi}{4}}$. Correction

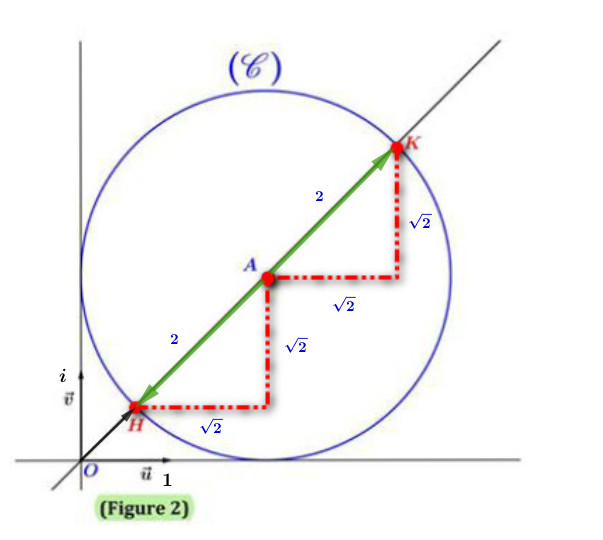    On a $z_A=2(1+i)$ et $\mathscr{C}$ cercle de centre $A$ et de rayon $2$ alors :
    $\text{Aff}\left( \overrightarrow{HA} \right)=\text{Aff}\left( \overrightarrow{AK} \right)=\sqrt{2}(1+i)$
    D'où $\text{Aff}\left( \overrightarrow{OH} \right)=\text{Aff}\left( \overrightarrow{OA}-\overrightarrow{HA} \right)=2(1+i)-\sqrt{2}(1+i)$
    et $\text{Aff}\left( \overrightarrow{OK} \right)=\text{Aff}\left( \overrightarrow{OA}+\overrightarrow{AK} \right)=2(1+i)+\sqrt{2}(1+i)$
    

    Donc $z_H=(2-\sqrt{2})(1+i)=(2-\sqrt{2})\sqrt{2}e^{i\frac{\pi}{4}}=(2\sqrt{2}-2)e^{i\frac{\pi}{4}}$
    et $z_K=(2+\sqrt{2})(1+i)=(2+\sqrt{2})\sqrt{2}e^{i\frac{\pi}{4}}=(2\sqrt{2}+2)e^{i\frac{\pi}{4}}$

  • 2°) A tout point $M$ d'affixe $z\neq 0$, on associe le point $M'$ d'affixe $z'$ tel que : $z'=\dfrac{-4}{z}$.
    1. (a) Montrer que pour tout point $M$ distinct de $O$ on a : $OM\times OM'=4$. Rappel

       Module d'un nombre complexe

       Dons un repère orthonormé du plan $\left( O,\vec{u},\vec{v} \right)$ du plan deux points $M$ et $N$ d'affixes respectives $z_M$ et $z_N$ alors : $MN=|z_N-z_M|$ d'où $OM=|z_M|$.
       Correction

       On a $OM=|z_M|=|z|$ et $OM'=|z_M'|=\left| \dfrac{-4}{z} \right|=\dfrac{4}{|z|}$ alors :
       

       $OM\times OM'=|z|.\dfrac{4}{|z|}=4$ pour tout $z\neq 0$.

    2. (b) Montrer que pour tout point $M$ distinct de $O$ on a : $\left( \widehat{\vec{u},\overrightarrow{OM'}} \right)\equiv \pi -\left( \widehat{\vec{u},\overrightarrow{OM}} \right) [2\pi]$ Rappel

       Proprétés d'un argument d'un nombre complexe non nul

       
       Correction

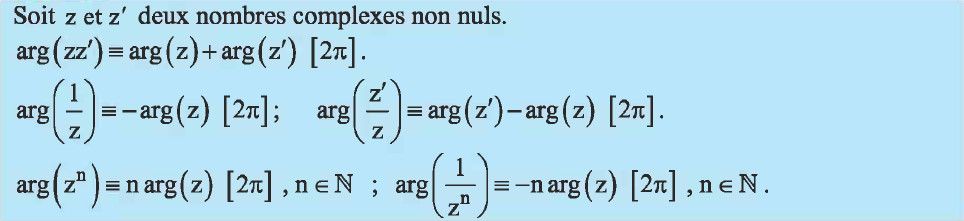
       Pour tout point $M$ distinct de $O$ $(z\neq 0)$ on a : $\begin{eqnarray} \left( \widehat{\vec{u},\overrightarrow{OM'}} \right) & \equiv & arg(z') [2\pi] \\ & \equiv & arg\left( \dfrac{-4}{z} \right) [2\pi] \\ & \equiv & arg\left( \dfrac{-1}{z} \right) [2\pi]\\ & \equiv & \pi + arg\left( \dfrac{1}{z} \right) [2\pi]\\ & \equiv & \pi - arg( z ) [2\pi] \end{eqnarray}$

       Donc pour tout point $M$ distinct de $O$ on a : $\left( \widehat{\vec{u},\overrightarrow{OM'}} \right)\equiv \pi -\left( \widehat{\vec{u},\overrightarrow{OM}} \right) [2\pi]$

  • 3°) Soient $z_H'$ et $z_K'$ les affixes respectives de $H'$ et $K'$ tels que : $z_H'=\dfrac{-4}{z_H}$ et $z_K'=\dfrac{-4}{z_K}$.
    1. (a) Montrer que $z_H'=\left( 2\sqrt{2}+2 \right)e^{i\frac{3\pi}{4}}$ et $z_K'=\left( 2\sqrt{2}-2 \right)e^{i\frac{3\pi}{4}}$. Rappel

       Ecriture exponentielle d'un nombre complexe

       
       Correction

       On a $|z_H'|\times|z_H|=4$ de même $|z_K'|\times|z_K|=4$ alors $|z_H'|=\dfrac{4}{2\sqrt{2}-2}=2\sqrt{2}+2$ et $|z_K'|=\dfrac{4}{2\sqrt{2}+2}=2\sqrt{2}-2$.
       $\begin{eqnarray} arg(z_H') & \equiv & \pi - arg(z_H) [2\pi]\\ & \equiv & \pi - \dfrac{\pi}{4} [2\pi]\\ & \equiv & \dfrac{3\pi}{4} [2\pi] \end{eqnarray}$ de même $\begin{eqnarray} arg(z_K') & \equiv & \pi - arg(z_K) [2\pi]\\ & \equiv & \pi - \dfrac{\pi}{4} [2\pi]\\ & \equiv & \dfrac{3\pi}{4} [2\pi] \end{eqnarray}$

       Donc $z_H'=\left( 2\sqrt{2}+2 \right)e^{i\frac{3\pi}{4}}$ et $z_K'=\left( 2\sqrt{2}-2 \right)e^{i\frac{3\pi}{4}}$

    2. (b) Construire les points $H'$ et $K'$. (justifier) Construction

       Construction des points $H'$ et $K'$ sur l'annexe (figure 2)

       Justification

       Puisque $z_H'=\left( 2\sqrt{2}+2 \right)e^{i\frac{3\pi}{4}}$ et $z_K'=\left( 2\sqrt{2}-2 \right)e^{i\frac{3\pi}{4}}$ alors $OH'=OK$ et $OK'=OH$ de plus :
       $\begin{eqnarray} \left( \widehat{\overrightarrow{Ok},\overrightarrow{OH'}} \right) & \equiv & \dfrac{3\pi}{4} - \dfrac{\pi}{4} [2\pi]\\ & \equiv & \dfrac{\pi}{2} [2\pi] \end{eqnarray}$ et $\begin{eqnarray} \left( \widehat{\overrightarrow{OH},\overrightarrow{OK'}} \right) & \equiv & \dfrac{3\pi}{4} - \dfrac{\pi}{4} [2\pi]\\ & \equiv & \dfrac{\pi}{2} [2\pi] \end{eqnarray}$

       D'où $H'$ et $K'$ sont les images respectivement de $K$ et $H$ par la rotation directe de centre $O$ et d'angle $\dfrac{\pi}{2}$.

Exercice N°3

Dans la figure ci-joite $\textbf{(Figure 3)}$, $(O,\vec{u} ,\vec{v})$ est un repère orthonormé direct du plan et $A$ un point du cercle de centre $O$ et de rayon $2$ tel que $\left( \widehat{\vec{u},\overrightarrow{OA}} \right)\equiv \theta [2\pi]$ où $\theta \in \left] 0;\dfrac{\pi}{2} \right[$. On désigne par $a$ l'affixe du point $A$.

• 1°) Donner, à laide de $\theta$, l'écriture exponentielle de chacun des nombres complexes : $a, -\dfrac{1}{\overline{a}}$ et $\dfrac{a^2}{\overline{a}}$. Rappel

  Ecriture exponentielle d'un nombre complexe

  
  Correction

  On a $A$ un point d'affixe $a$ avec $A\in \mathscr{C}(O,2)$ d'où $|a|=2$ et $arg(a)\equiv \theta \, [2\pi]$ alors $\colorbox{yellow}{$a=2e^{\mathrm{i}\theta}$}$
  $B$ un point d'affixe $-\dfrac{1}{\overline{a}}$ alors $z_B=-\dfrac{1}{\overline{2e^{\mathrm{i}\theta}}}=e^{i\pi}\dfrac{1}{2e^{-\mathrm{i}\theta}}=\colorbox{yellow}{$\dfrac{1}{2}e^{\mathrm{i}(\pi+\theta)}$}$
  $C$ un point d'affixe $\dfrac{a^2}{\overline{a}}$ alors $z_C=\dfrac{(2e^{\mathrm{i}\theta})^2}{\overline{2e^{\mathrm{i}\theta}}}=\dfrac{2^2e^{2\mathrm{i}\theta}}{2e^{-\mathrm{i}\theta}}=\colorbox{yellow}{$2e^{3\mathrm{i}\theta}$}$

• 2°)Construire sur l'annexe les points $B$ et $C$ d'affixes respectives $-\dfrac{1}{\overline{a}}$ et $\dfrac{a^2}{\overline{a}}$. Construction

  Construction des points $B$ et $C$ sur l'annexe (figure 3)

  Justification

  On a $B$ un point d'affixe $-\dfrac{1}{\overline{a}}=\dfrac{1}{2}e^{i(\theta+\pi)}$
  Alors :

  $B\in [AO)$ tel que $OB=\dfrac{1}{2}$

  De même $C$ un point d'affixe $\dfrac{a^2}{\overline{a}}=2e^{3i\theta}$
  Alors :

  $C\in \mathscr{C}(O,2)$ tel que $\left( \widehat{\vec{u},\overrightarrow{OC}} \right) \equiv 3\theta [2\pi]$

• 3°)
  1. (a) vérifier que $\dfrac{z_B-z_A}{z_C}=-\dfrac{5}{4}e^{-2i\theta} $. Correction

     On a $z_A=2e^{\mathrm{i}\theta}$, $z_B=\dfrac{1}{2}e^{\mathrm{i}(\pi+\theta)}$ et $z_C=2e^{3\mathrm{i}\theta}$ alors : $\begin{eqnarray} \dfrac{z_B-z_A}{z_C} & = & \dfrac{\dfrac{1}{2}e^{\mathrm{i}(\pi+\theta)}-2e^{\mathrm{i}\theta}}{2e^{3\mathrm{i}\theta}} \\ & = & \dfrac{-\dfrac{1}{2}e^{\mathrm{i}(\theta)}-2e^{\mathrm{i}\theta}}{2e^{3\mathrm{i}\theta}} \\ & = & -\dfrac{\dfrac{5}{2}e^{\mathrm{i}\theta}}{2e^{3\mathrm{i}\theta}} \\ & = & -\dfrac{5}{4}e^{\mathrm{i}\theta}e^{-3\mathrm{i}\theta} \\ & = & -\dfrac{5}{4}e^{-2i\theta} \end{eqnarray}$

  2. (b) En déduire la valeur de $\theta$ pour laquelle les droites $(AB)$ et $(OC)$ sont perpendiculaires. Simulation

     Détermination de $\theta$ pour que $(OA)\perp (OC)$

     Correction

     On a $\dfrac{z_B-z_A}{z_C}=-\dfrac{5}{4}e^{-2i\theta} $ Alors :
     $\begin{eqnarray} (OA)\perp (OB) & \Longleftrightarrow & -\dfrac{5}{4}e^{-2i\theta}\in \mathrm{i}\mathbb{R} \\ & \Longleftrightarrow & \dfrac{5}{4}e^{-2i(\theta +\pi)}\in \mathrm{i}\mathbb{R} \\ & \Longleftrightarrow & -2\theta +\pi \equiv \dfrac{\pi}{2} [2\pi] \\ & \Longleftrightarrow & -2\theta \equiv -\dfrac{\pi}{2} [2\pi] \\ & \Longleftrightarrow & \theta \equiv \dfrac{\pi}{4} [2\pi] \end{eqnarray}$ Rappel

     Proprété

     

     
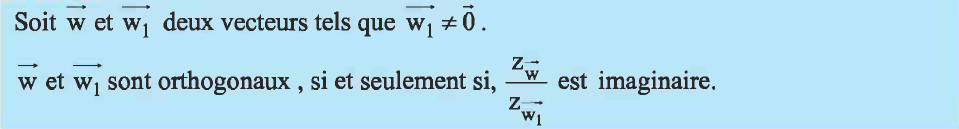
     Puisque $\theta \in \left] 0;\dfrac{\pi}{2} \right[$ Alors

     $\theta =\dfrac{\pi}{4}$